著名的乌鸦悖论:用一张白纸就可以证明乌鸦都是黑色的?
#头条创作挑战赛#
相信大家都听过“天下乌鸦一般黑”这句话,那么天下的乌鸦到底是不是黑色的呢?
今天,我来给大家讲解一个非常有意思的问题,即乌鸦悖论,也称亨佩尔的乌鸦、亨佩尔悖论,由20世纪40年代德国逻辑学家卡尔·古斯塔夫·亨佩尔(Carl Gustav Hempel)提出,旨在说明归纳法违反直觉。

Carl Gustav Hempel

故事是这样的:从前有一个老头每次出门都能在家门口看到许多黑色的乌鸦,他突发奇想:是不是所有的乌鸦都是黑色的?于是他提出了自己的假设“所有乌鸦都是黑色的”。今后他为了证实这个想法,每天都早早出门去观察乌鸦。每天看呀看呀,连饭都不吃了,直到观察了成千上万只乌鸦,这个老头越来越确信:所有乌鸦都是黑的!
每次观察后,对“所有乌鸦都是黑的”的信任度会逐渐提高。由归纳法原理看起来“所有乌鸦都是黑色的”这个假设是合理的。
(现实中并不是所有乌鸦都是黑色,如白颈乌鸦,美洲乌鸦)

非洲白颈乌鸦
现在我们知道有足够多的实例去证明“所有乌鸦都是黑色的”这个假设,那这个假设即为正确的。
人类历史上有很多定理都是通过大量的实验与观察得到的,如地心引力。那么接下来来到我们重头戏:如何用一张白纸就可以证明乌鸦都是黑色的?
想要解决这个问题,我们还要引入一个逻辑上的概念“逆否命题”:
原命题为:若a,则b。逆否命题为:若非b,则非a。逆否命题与原命题是等价的
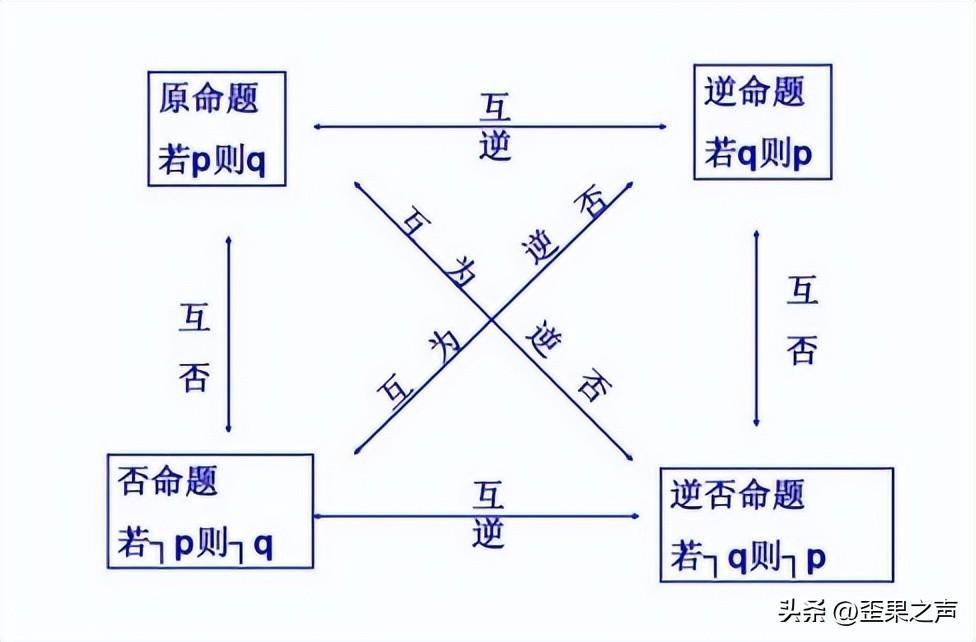
看不懂也没有关系,我举几个例子你就明白了:
原命题:“张三现在在吃饭” 等价于逆否命题 “若一个人现在不在吃饭,那么他就不是张三”
原命题:“若现在在下雨,则我穿雨衣” 等价于逆否命题 “若我不穿雨衣,则现在不下雨”
好了,接下我们再来看看我们要讨论的命题“所有乌鸦都是黑色的”,这个命题等价于它的逆否命题“所有不是黑色的东西不是乌鸦”,那我们只要证明这个逆否命题是正确合理的,那么也就证明原命题的正确的
现在那个天天观察乌鸦的老头在观察了一天乌鸦后,满意地回到家,发现了孙子正准备用桌子上的白纸画画,看着这张白纸,老头忽然想到自己的一直在证明的命题“所有乌鸦都是黑色的”不就是等价于“所有不是黑色的东西不是乌鸦”这个命题嘛,眼前的这张白纸,不是黑色的,也不是乌鸦,这不就是一个可以证明“所有不是黑色的东西不是乌鸦”这个命题的例子吗?
老头再看看桌子上的红苹果,苹果不是黑色的,也不是乌鸦,孙子五颜六色的画笔,不是黑色的,也不是乌鸦,头顶挂着的灯,不是黑色的,也不是乌鸦……几乎所有东西都可以充当“所有不是黑色的东西不是乌鸦”这个论点的论据,也就可以证明了与其等价的原命题“所有乌鸦都是黑色的”!原来足不出户就可以证明所有乌鸦都是黑色,老头高兴的想到,从此之后,这位热衷于观察乌鸦老头再也没有出过门去看乌鸦了。
故事就讲到这,大家看完是不是觉得非常的神奇?
用大量正确的例子即可证明一个假设的正确,这在逻辑学上是公认的,但是这也会导致“用一张白纸就可以证明所有乌鸦都是黑色”的荒谬的结果,
有些哲学家质疑“等价原理”。也许红苹果能够增加对论断“所有不是黑色的东西不是乌鸦”的信任度,而不增加对 “所有乌鸦都是黑色的”信任,这样就不会出现这种结果了,但是这样做又会违反人们对归纳论证的常识,所以这个问题直至今日仍会有许多思考家为其痴迷。
但我在这里举另外一个例子供大家思考:假设“没有一个人的身高会超过3m”,这个假设在通过大量观察后证明其的合理性
但这时候突然蹦出了一个2.8m高的人类,虽然他的身高仍在假设的范围内,仍可以充当一个论据提高这个假设的可信度。
但这时人们会想“既然有2.8m的人,3m多高的人会不会也存在呢?”那这个因为这个例子的出现,原假设的可信度究竟是高了还是低了呢?欢迎大家在评论区探讨!
